Gaudi-GBLR: Differentiable, and Generalized Block Low-Rank Matrix Format for Efficient DNNs Gaudi-GBLR: Differentiable, and Generalized Block Low-Rank Matrix Format for Efficient DNNs | Changwoo Lee

Gaudi-GBLR: Differentiable, and Generalized Block Low-Rank Matrix Format for Efficient DNNs

Changwoo Lee, Hun-Seok Kim
University of Michigan
ICLR 2024
Paper arXiv

Introduction

Deep Neural Networks (DNNs) are getting bigger and bigger. A way to reduce the complexity of the DNNs is to use the structured weight matrices, like Low-Rank or Sparse matrices.

This work introduces a Gaudi-GBLR matrix, which is a (G)eneralized (B)lock (L)ow-(R)ank Matrix with (Gau)ssian-(Di)richlet Function.

  • Expressiveness. Gaudi-GBLR includes other structured matrices such as Low-Rank, Block-Low-Rank, and Block-Sparse matrices.
  • Differentiability. The structure of the Gaudi-GBLR is differentiable! The efficient structure of the weight matrix is learned from data. So the efficient DNN can be learned from scratch!
  • Layer-wise Optimization. The structure (and the complexity) is optimized in a layer-wise manner. The less important, the less complexity.

Generalized Block Low-Rank (GBLR) Matrix

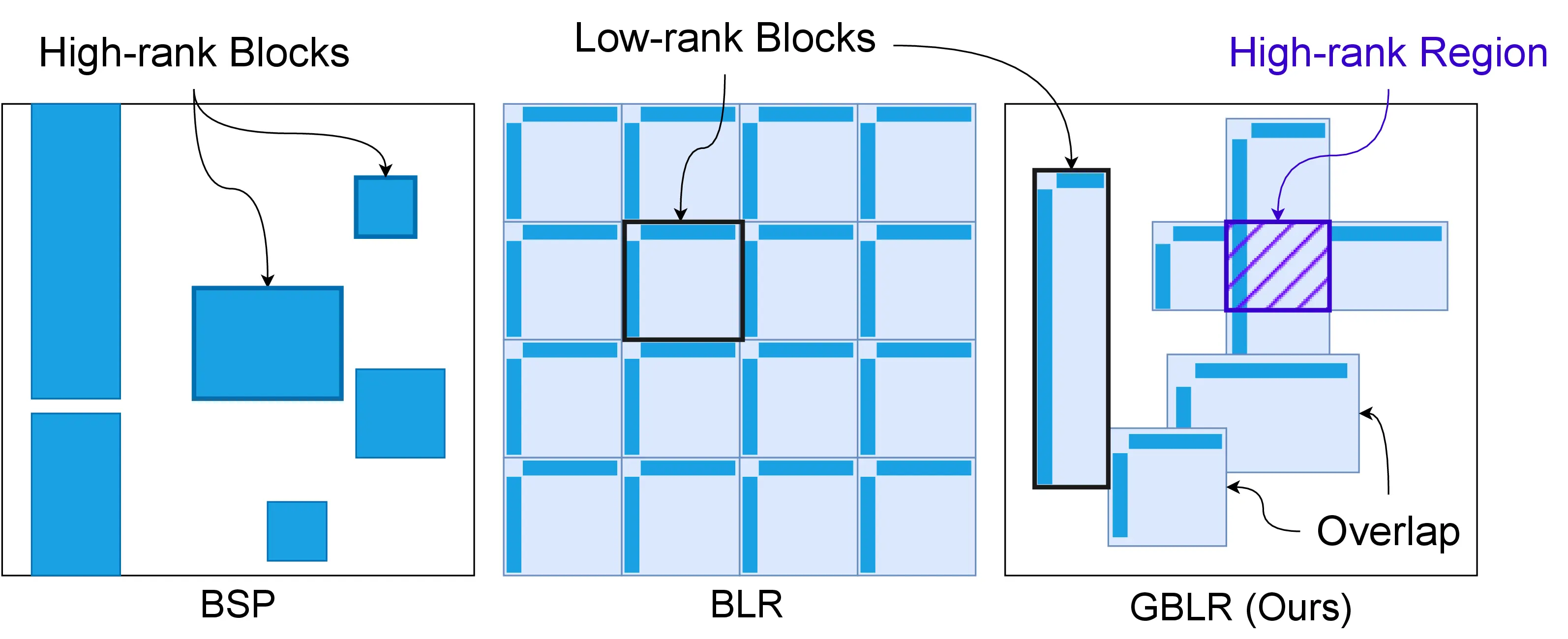
A GBLR matrix is a generalized version of the Block Low-Rank (BLR) matrix. Unlike the BLR structure, a GBLR matrix is composed of multiple overlapping low-rank blocks. Notably, the GBLR structure includes multiple important efficient matrix structures. In our paper, we analyzed that the GBLR format contains Low-Rank, Block-Sparse, Block-Low-Rank matrices of the same complexity for the matrix-vector product.

gblr

The key idea is to learn the location and the area of each block from data. Once they are found, the matrix-vector product can be done faster on the specialized hardware. We left demonstrating the actual speedup as future work.

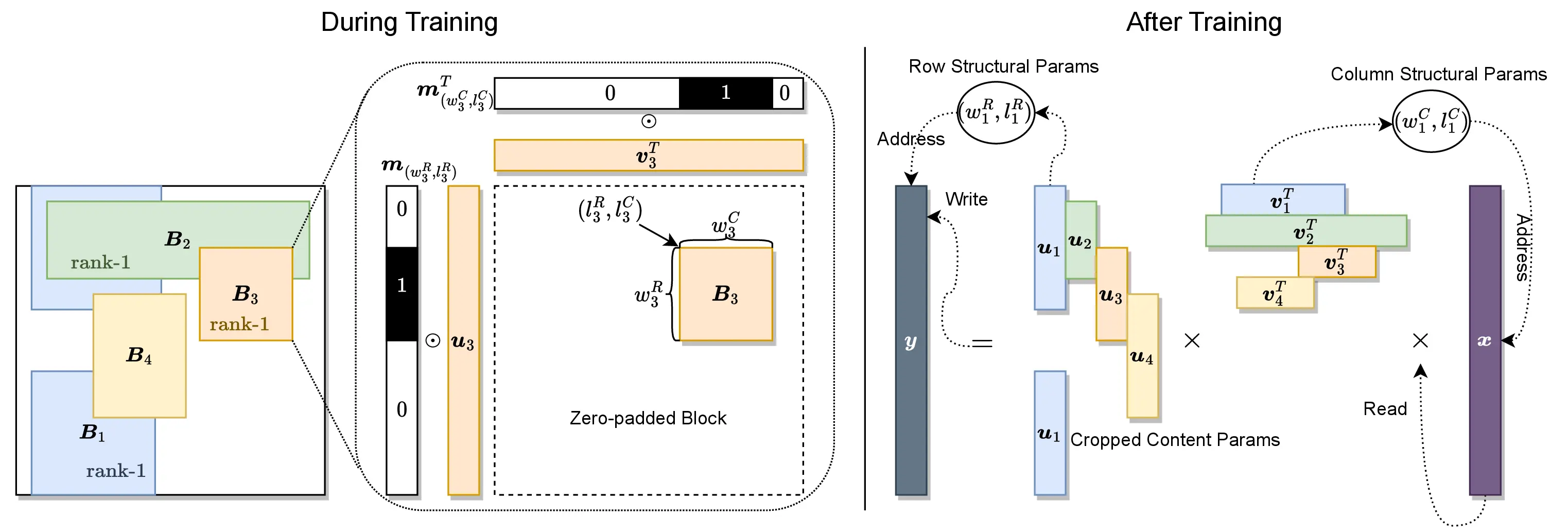
gblr-detailed

Gaussian-Dirichlet (Gaudi) Function for Differentiability

Unfortunately, optimizing the structural (location and area) parameters of the GBLR matrix is not easy. The parameters are defined in the discrete space, and non-differentiable.

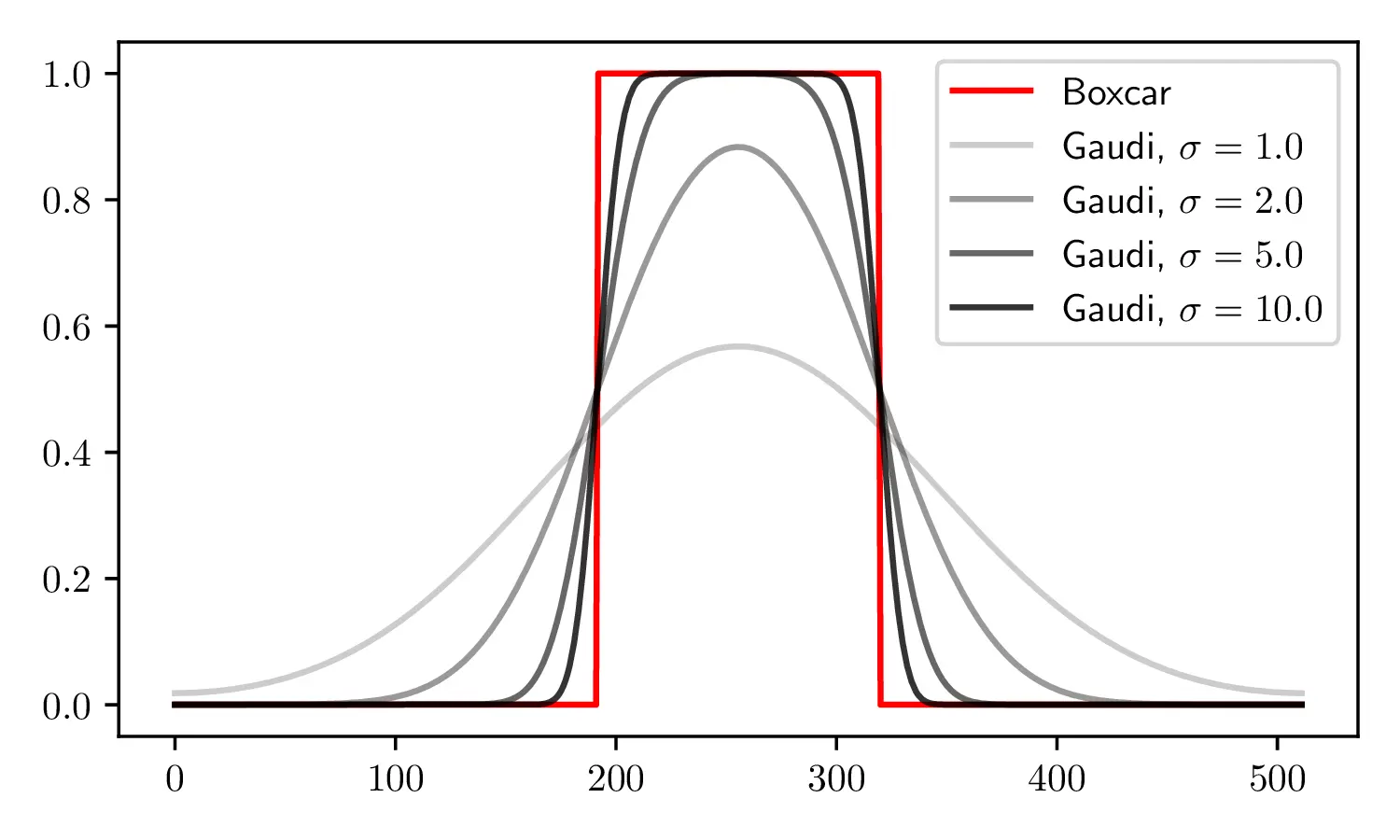
Here, we circumvent the problem by defining the structural parameter in the frequency domain. The location and the width and height of the low-rank block appear explicitly and differentiably in the form of the Dirichlet function, which is the DFT pair of the Boxcar function. By taking a Gaussian filter for the numerical stability, we obtain a Gaussian-Dirichlet (Gaudi) function to indicate the position of the low-rank block.

gaudi

Layer-wise Optimization

Intuitively, we don’t think all layers are equally important. Some layers might contribute less than others, which indicates that less important layers can be compressed more.

Unfortunately, it has been very time-consuming to allocate different number of computations for each layer since the search space is discrete and the problem is NP-hard.

In contrast, with the GBLR format, the layer-wise structural parameter optimization can be easily done because we can update the structural parameters by Stochastic Gradient Descent (SGD).

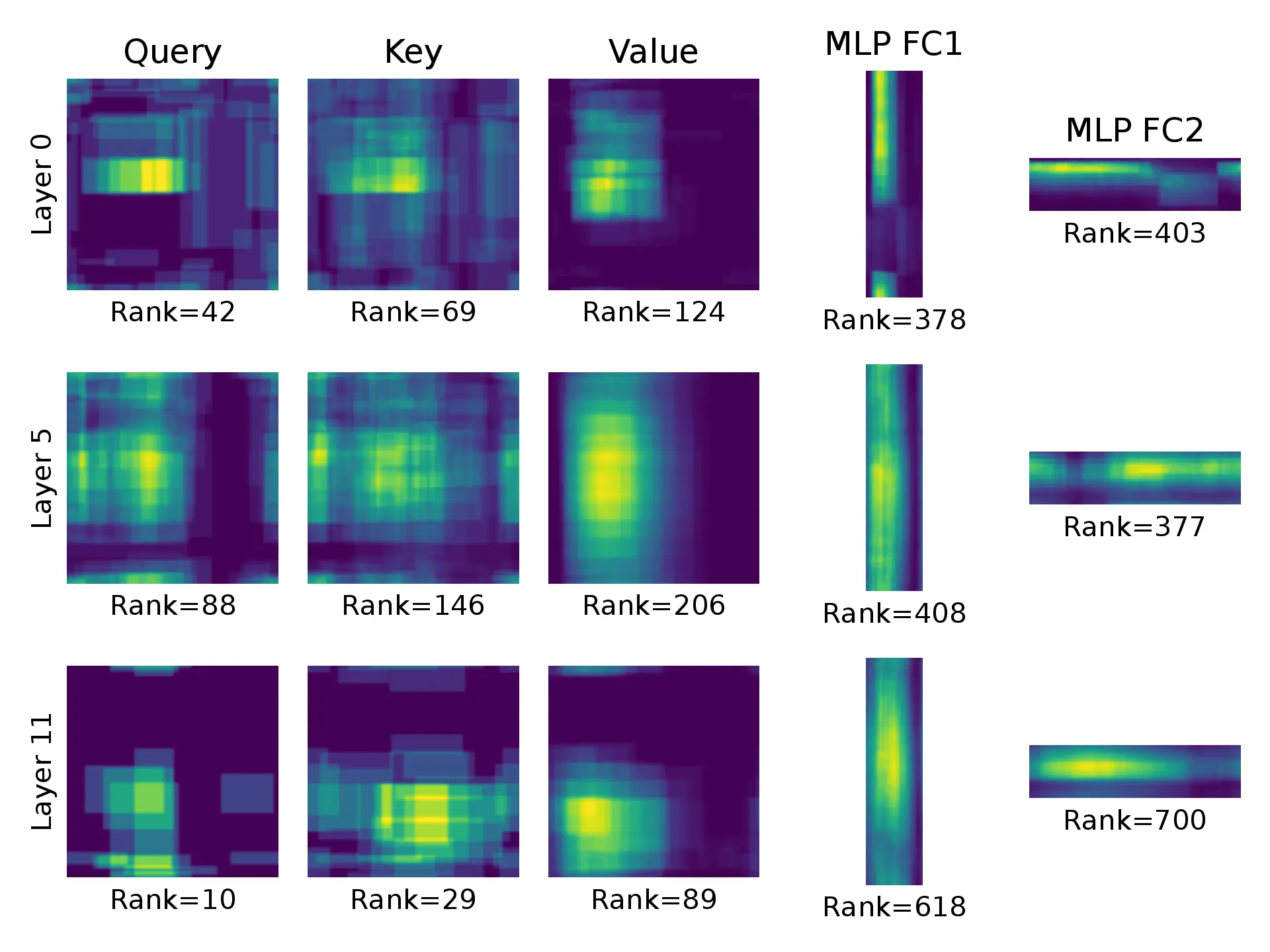
The figure below illustrates the learned Gaudi-GBLR weight matrices of the ViT-Base model trained on ImageNet. The brighter, the more overlapping low-rank blocks. Each weight has different rank and structure, which are found during the training process by SGD.

gaudi

BibTeX

@inproceedings{lee2023differentiable,
  title={Differentiable Learning of Generalized Structured Matrices for Efficient Deep Neural Networks},
  author={Lee, Changwoo and Kim, Hun-Seok},
  booktitle={The Twelfth International Conference on Learning Representations},
  year={2024},
  url={https://openreview.net/forum?id=pAVJKp3Dvn}
}